CAsimulations: Modelación de las dinámicas de la propagación de una enfermedad usando AC
CAsimulations proporciona una manera de simular fenómenos asociados con la propagación de enfermedades, basándose en modelos SIS, SIR y algunas de sus variaciones implementadas en autómatas celulares en Python. CAsimulations incluye una gran variedad de utilidades para análisis epidemiológicos tales como la capacidad de definir la condición inicial de frontera del sistema, la condición inicial de dispersión de los individuos infectados, variaciones y comparaciones con respecto al cambio de escala y al cambio de frontera del sistema, variaciones promedio para un número arbitrario de simulaciones, entre otros.
Si desea profundizar sobre los fundamentos detrás de la lógica implementada en la librería, puede dirigirse al documento principal.
Para importar la librería, ejecute el siguiente comando pip en su entorno de Python:
pip install -i https://test.pypi.org/simple/ CAsimulation
Una vez instalada, podemos proceder a cargar la librería, para lo cual tendrá que ejecutar el siguiente script
from CAsimulation import epidemiologicalModelsInCA as ca
Con la línea anterior podrá acceder a los módulos que le brindarán la posibilidad de implementar las herramientas descritas en el documento de una manera fácil y rápida. Si desea analizar detalladamente las funciones de la librería, puede dirigirse al enlace o implementar los módulos de manera individual.
Observación: Los valores que se muestran sobre las matrices que describen las evoluciones del sistema, son precisamente los indicadores de cada estado. El indicador para cada estado se muestra en la siguiente tabla:
| Estado | Indicador |
|---|---|
| Susceptible | 0 |
| Infectado | 1 |
| Recuperado | 2 |
| Muerto | 3 |
| Espacio vacío | -1 |
A continuación presentaremos la documentación de cada uno de los módulos de la librería, si desea consultar ejemplos particulares puede consultar directamente el documento principal o los ejemplos particulares.
Los módulos de la siguiente manera:
- AgeManagement
- CellManagement
- CellSpaceConfiguration
- CompartmentalModelsInEDOS
- DataManager
- Models
- NeighborhoodManager
- PlotsManager
- SystemVisualization
- epidemiologicalModelsInCA
AgeManagement
El móduloAgeManagement se encarga de controlar todos los procesos que tengan que ver con el manejo de las edades de algún conjunto de células, esto en particular para los modelos con natalidad y mortalidad; y los que tienen en cuenta la muerte por enfermedad, ambos descritos en el documento principal.
Con este módulo podremos crear a la matriz de edades, dados los rangos y las proporciones de edades en el sistema, y, por otro lado, tenemos a las evoluciones para la matriz de edades descritas en los modelos que implementan esta característica. Para importar este módulo puede usar la siguiente línea:
from CAsimulation import AgeManagement as am
Para usar la clase AgesMatrix debe establecer inicialmente los rangos de edades y sus proporciones en el sistema, es decir, que porcentaje de los individuos tiene cierto rango de edad; y, por otro lado, será necesario que ya tenga definido un espacio de células.
from CAsimulation import epidemiologicalModelsInCA as em
# Espacio de células
cellSpace = em.CellSpace(5,5) # Sistema con 25 células (dim(cellSpace) = 5x5)
# Rangos de edades
ranges = [[0,20,0.5], [21,60,0.25], [61,100,0.25]] # El 50% tienen entre 0 y 20, el 25% entre
# 21 y 60 , y el 25% restante tiene entre 61 y 100
# Matriz de edades
agesMatrix = am.AgesMatrix(ranges, cellSpace)
No es necesario utilizar un script adicional, ya que al instanciar la clase AgesMatrix se genera automáticamente la matriz de edades. Para ver dicha matriz, ejecute el siguiente comando:
agesMatrix.agesMatrix
>>> array([[52., 0., 52., 52., 52.],
[15., 75., 12., 8., 41.],
[ 5., 7., 10., 7., 7.],
[12., 71., 5., 52., 74.],
[16., 24., 7., 53., 15.]])
Una vez tenemos definida la matriz de edades, podremos aplicar las reglas de evolución que tienen en cuenta las edades de las células. En particular nos encontramos con el manejo de edades descrito en la regla para modelos con natalidad y mortalidad, y los modelos con muerte por enfermedad.
Debido a que una de las características de nuestra propuesta es considerar diferentes rangos de edades para aplicar las reglas de evolución que definimos en el documento, debemos ser capaces de identificar a los individuos que poseen cierta edad. Esto lo podremos hacer con la siguiente línea de código:
# Parámetros para instanciar la clase AgeMatrixEvolution
birthRate = 0.02
annualUnit = 365
mortabilityRatesByAgeRange = [[1,20,0.05],[21,100,0.025]]
ages = agesMatrix.agesMatrix
ageMatrixManagement = am.AgeMatrixEvolution(ages, birthRate, annualUnit, mortabilityRatesByAgeRange)
ageMatrixManagement.ageGroupPositions(42, 65) # Coordenadas de células con edades entre 42 y 65 "años"
>>> [[0, 0], [0, 2], [0, 3], [0, 4], [3, 3], [4, 3]]
Para aplicar la regla que describe la evolución para la matriz de edades considerando la natalidad y la mortalidad, debemos establecer la iteración sobre la que estamos aplicando el modelo. Si esta iteración es múltiplo de annualUnit diremos que las células cumplen un ciclo temporal (años, meses, décadas, minutos, etc). El siguiente script nos muestra la manera adecuada de implementar esta característica:
ageMatrixManagement.evolutionRuleForAges(10)
>>> array([[52., 0., 52., 52., 52.],
[15., 75., 12., 8., 41.],
[ 5., 7., 10., 7., 7.],
[12., 71., 5., 52., 74.],
[16., 24., 7., 53., 15.]])
ageMatrixManagement.evolutionRuleForAges(365*2)
>>> array([[53., 1., 53., 53., 53.],
[16., 76., 13., 9., 42.],
[ 6., 8., 11., 8., 8.],
[13., 72., 6., 53., 75.],
[17., 25., 8., 54., 16.]])
Para aplicar la regla que describe la evolución para las edades del sistema de células considerando la muerte por enfermedad podemos ejecutar el siguiente script:
cellSpace = cellSpace.initialLocationOfInfected(0.5) # Suponemos que el 50% de la población posee la enfermedad
cellSpace.system
>>> array([[1., 0., 1., 1., 0.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 0.],
[0., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
deathByDiseaseRatesByAgeRanges = [[1,50,0.2], [51,100,0.4]]
systemAfterEvolution, agesMatrixAfterEvolution = ageMatrixManagement.deathByDiseaseRule(cellSpace, deathByDiseaseRatesByAgeRanges)
systemAfterEvolution.system
>>> array([[1., 3., 3., 3., 0.],
[1., 1., 3., 3., 1.],
[1., 1., 3., 1., 0.],
[0., 1., 3., 3., 3.],
[1., 1., 1., 3., 3.]])
agesMatrixAfterEvolution
>>> array([[52., 0., 0., 0., 52.],
[15., 75., 0., 0., 41.],
[ 5., 7., 0., 7., 7.],
[12., 71., 0., 0., 0.],
[ 0., 24., 7., 0., 0.]])
CellManagement
Con el módulo CellManagement podrá darle manejo a propiedades espaciales que le permitan manipular o redefinir la lógica para el comportamiento mismo de las células. Adicionalmente, tendremos la capacidad de acceder a un conjunto de células, vía sus coordenadas, dado un estado específico del modelo. Para importar el módulo CellManagement puede usar la siguiente línea:
from CAsimulation.CellManagement import CellManagement as cm
Con este módulo será posible generar una copia de un sistema a partir de uno existente, con la posibilidad de expandir su dimensión. Esto lo podremos hacer con la función InsideCopy. Para implementar esta función podemos usar un script como el siguiente:
from CAsimulation import epidemiologicalModelsInCA as em
cellSpace = em.CellSpace(5,5).initialLocationOfInfected(0.4)
cellSpace.system
>>> array([[0., 1., 0., 0., 0.],
[1., 1., 0., 1., 1.],
[0., 0., 0., 0., 1.],
[0., 1., 0., 0., 0.],
[0., 1., 0., 0., 1.]])
cellSpaceCopy = cm.CellManagement(cellSpace).InsideCopy(1, 3)
cellSpaceCopy.system
>>> array([[-1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1.],
[-1., -1., -1., 0., 1., 0., 0., 0., -1., -1., -1.],
[-1., -1., -1., 1., 1., 0., 1., 1., -1., -1., -1.],
[-1., -1., -1., 0., 0., 0., 0., 1., -1., -1., -1.],
[-1., -1., -1., 0., 1., 0., 0., 0., -1., -1., -1.],
[-1., -1., -1., 0., 1., 0., 0., 1., -1., -1., -1.],
[-1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1.]])
Debemos resaltar que los valores -1 indican espacios vacíos, es decir, celdas que no interactúan de ninguna forma con las demás.
Si ahora lo que desea es conocer las coordenadas por estado, puede usar la función StateCoordinates, la cual toma como parámetro al indicador de un estado específico y retorna una lista de coordenadas, como se muestra a continuación:
cm.CellManagement(cellSpace).StateCoordinates(1) # Coordenadas de las células infectadas
>>> [[0, 1], [1, 0], [1, 1], [1, 3], [1, 4], [2, 4], [3, 1], [4, 1], [4, 4]]
Puede también determinar el porcentaje de individuos con un estado específico y visualizar como distribuirían, si deseará por ejemplo, establecer una condición inicial particular. Para esto usaremos la función StatePercentageInSpace, la cual se implementa de la siguiente manera:
cm.CellManagement(cellSpace).StatePercentageInSpace(2, 8, 1)
>>> [0, 0, 0, 0, 1, 1, 0]
cm.CellManagement(cellSpace).StatePercentageInSpace(2, 10, 2, -1)
>>> [-1, -1, 2, 2, -1, -1, -1, -1, -1]
La última función que encontraremos en este módulo nos permite definir la condición inicial de una manera sencilla con la característica de distribuir aleatoriamente a las células dado el porcentaje inicial de infectados.
cellSpaceWithInitialCondition = cm.CellManagement(cellSpace).InitialCondition(0.4)
cellSpaceWithInitialCondition.system
>>> array([[0., 1., 0., 0., 1.],
[1., 1., 0., 1., 1.],
[0., 1., 1., 0., 1.],
[1., 1., 1., 0., 0.],
[0., 1., 0., 0., 1.]])
CellSpaceConfiguration
Como su nombre lo indica, el módulo CellSpaceConfiguration será el encargado de las configuraciones sobre el espacio de células, como por ejemplo, las condiciones iniciales o las condiciones de frontera. Para importar el módulo CellSpaceConfiguration puede usar la siguiente línea:
from CAsimulation.CellSpaceConfiguration import CellSpaceConfiguration as cc
Podemos definir de tres maneras diferentes al espacio de células: la primera genera un espacio completo en el sentido de que no hay celdas vacías; la segunda manera crea una región de células que pueden interactuar en la esquina superior izquierda, dejando una cantidad determinada de espacios vacíos; y la última, permite definir varias regiones de células que interactuan en diferentes ubicaciones. Esto será de vital importancia si desea analizar el comportamiento de alguna enfermedad en espacios con diferentes condiciones de frontera.
Para generar estos espacios puede ejecutar las siguientes líneas, dependiendo del contexto en el contexto en el que este definiendo su espacio de células:
csc1 = cc.CellSpaceConfiguration(3,3) # Espacio de 9 células sin celdas vacías
csc2 = cc.CellSpaceConfiguration(3,3,5,6) # Espacio de 9 células ubicado en una matriz de espacios
# vacíos de dimensión 5x6
csc3 = cc.CellSpaceConfiguration(3,3,7,7,1,2) # Espacio de 9 células ubicado en una matriz de
# espacios vacíos de dimensión 7x7 ubicado en la
# posición 1,2
Este módulo nos permite observar la construcción de los espacios y los parámetros con los que se define, independientemente de la manera en la que se define:
# Parámetros con los que se define el espacio de células
csc1.basicParameters()
>>> (3, 3, -1, -1, 0, 0)
csc1.system
>>> array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
csc2.system
>>> array([[ 0., 0., 0., -1., -1., -1.],
[ 0., 0., 0., -1., -1., -1.],
[ 0., 0., 0., -1., -1., -1.],
[-1., -1., -1., -1., -1., -1.],
[-1., -1., -1., -1., -1., -1.]])
csc3.system
>>> array([[-1., -1., -1., -1., -1., -1., -1.],
[-1., -1., 0., 0., 0., -1., -1.],
[-1., -1., 0., 0., 0., -1., -1.],
[-1., -1., 0., 0., 0., -1., -1.],
[-1., -1., -1., -1., -1., -1., -1.],
[-1., -1., -1., -1., -1., -1., -1.],
[-1., -1., -1., -1., -1., -1., -1.]])
Una de las cualidades de este módulo es que permite definir sistemas no necesariamente regulares, lo que a su vez nos brinda la capacidad por ejemplo, de aislar individuos bajo diferentes supuestos. Para implementar la función rectangularBoundary debe tener en cuenta que los dos primeros parámetros corresponden a la dimensión de una segunda región de células que pueden interactuar; y los dos últimos parámetros indican la ubicación de esta segunda región.
cellSystem = csc3.rectangularBoundary(2,3,4,3) # Sistema de dimensión 2x3 ubicado en la posición 4,3
cellSystem
>>> array([[-1., -1., -1., -1., -1., -1., -1.],
[-1., -1., 0., 0., 0., -1., -1.],
[-1., -1., 0., 0., 0., -1., -1.],
[-1., -1., 0., 0., 0., -1., -1.],
[-1., -1., -1., 0., 0., 0., -1.],
[-1., -1., -1., 0., 0., 0., -1.],
[-1., -1., -1., -1., -1., -1., -1.]])
Por último, presentamos a la función que nos permitirá definir una condición inicial de población infectada con la posibilidad de partir de una ubicación específica, como se muestra en los siguientes fragmentos de código:
csc1.initialLocationOfInfected(0.5, "center") # 50% de la población en el centro, esta infectada
>>> array([[0., 0., 0.],
[0., 1., 0.],
[0., 0., 0.]])
csc1.initialLocationOfInfected(0.5).system # El 50% del total de la población posee la enfermedad
>>> array([[0., 1., 1.],
[1., 0., 1.],
[0., 0., 1.]])
csc3.initialLocationOfInfected(0.5).system # El 50% del total de la población posee la enfermedad
# sin importar la regularidad del espacio de células
>>> array([[-1., -1., -1., -1., -1., -1., -1.],
[-1., -1., 1., 0., 1., -1., -1.],
[-1., -1., 1., 0., 0., -1., -1.],
[-1., -1., 0., 0., 0., -1., -1.],
[-1., -1., -1., 0., 1., 1., -1.],
[-1., -1., -1., 1., 0., 1., -1.],
[-1., -1., -1., -1., -1., -1., -1.]])
CompartmentalModelsInEDOS
Con el módulo CompartmentalModelsInEDOSpodremos aplicar el método de Euler para ecuaciones diferenciales y visualizar sus soluciones, en nuestro caso lo usaremos para observar los comportamientos descritos por los modelos compartimentales clásicos, sin embargo, el lector puede implementarlo en el contexto sobre el que esté trabajando.
Puede importar esté módulo de la siguiente manera:
from CAsimulation import CompartmentalModelsInEDOS as ca
Antes de empezar a usar este módulo debemos definir el sistema de ecuaciones adecuadamente, como se muestra a continuación
# Parámetros del modelo:
alpha = 0.2
mu = 1/(75*365)
theta = 0.4
beta = 0.5
# Funciones del modelo:
def S_function(values, beta = beta, mu = mu, theta = theta):
S = values[0]; I = values[1]
return mu*(1 - S) + (1 - theta)*alpha*I - beta*S*I
def I_function(values, alpha = alpha, beta = beta, mu = mu, theta = theta):
S = values[0]; I = values[1]
return beta*S*I - (1 - theta)*alpha*I - mu*I
listOfFunctions = [S_function, I_function]
# Condiciones iniciales:
initialValues = [0.9, 0.1] # S_0 = 0.9; I_0 = 0.1
El módulo CompartmentalModelsInEDOS permite establecer la cantidad de iteraciones y el valor h empleado en el método de Euler.
# Se instancia el módulo
discreteSolutions = ca.CompartmentalModelsInEDOS(listOfFunctions, initialValues)
discreteSolutions.n_iterations(1100)
discreteSolutions.h(0.1)
Si desea visualizar los parámetros que está usando en su modelo, puede ejecutar la siguiente línea:
discreteSolutions.PrintParameters()
>>> h: 0.1
n_iterations: 1100
differentialEquations: [<function S_function at 0x7f5462cb14d0>,
<function I_function at 0x7f5462cb1200>]
Puede obtener las soluciones discretas del sistema que esté trabajando de dos formas: la primera le presenta el conjunto de coordenadas por iteración para estado del modelo; y la segunda le muestra los datos en forma de gráfica, brindándole la posibilidad de acceder a los datos.
# Conjunto de datos correspondiente a las soluciones del modelo
discreteSolutions.ModelSolutions()
>>> [[[0.9,
0.8967003652968036,
0.8933088972548366,
0.8898241746599574,
0.8862448313902722,
...],
[0.1,
0.10329963470319635,
0.10669110274516336,
0.1101758253400425,
0.11375516860972777,
...]],
range(0, 1100)]
# Gráfica de las soluciones del modelo
nameVariables = ["Susceptibles", "Infectados"]
colorOfVariables = ["yellow", "red"]
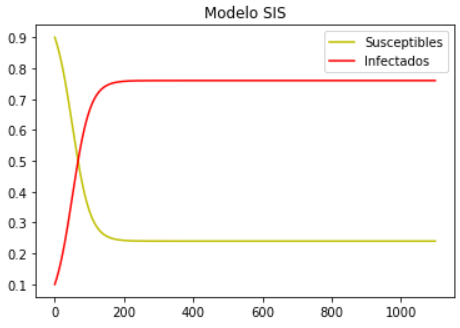
discreteSolutions.titlePlot = "Modelo SIS"
discreteSolutions.plotSolutions(nameVariables, colorOfVariables)
Si desea consultar más ejemplos, puede dirigirse al cuadernillo Modelos compartimentales clásicos.
DataManager
Este módulo será el encargado de darle manejo a todos los datos que puedan extraerse de las aplicaciones por iteración de cada uno de los modelos descritos en el documento principal. Para importar el módulo DataManager puede usar la siguiente línea:
from CAsimulation import DataManager as dm
En este módulo encontraremos a la clase SystemMetrics que nos permite extraer las métricas de cada iteración, luego de aplicar el modelo epidemiológico. Para instanciar esta clase inicialmente debemos crear un espacio de células y definir además, los estados para los cuales se extraerán las métricas.
csc = cc.CellSpaceConfiguration(3,3,7,7,1,2)
SISstates = [0, 1]
# Métricas para el modelo SIS
metricsWithoutEmptyCells = dm.SystemMetrics(csc, SISstates)
SISstatesWithEmptySpaces = [0, 1, -1]
# Métricas para el modelo SIS con espacios vacíos
metrics = dm.SystemMetrics(csc, SISstatesWithEmptySpaces)
Podemos extraer dos tipos de datos: las proporciones y las cantidades de individuos por estado:
# Proporciones
metricsWithoutEmptyCells.statusInTheSystem()
>>> [1.0, 0.0]
metrics.statusInTheSystem() # Porcentajes
>>> [0.30612244897959184, 0.0, 0.6938775510204082]
# Cantidades
metricsWithoutEmptyCells.statusInTheSystem(False)
>>> [9, 0]
metrics.statusInTheSystem(False)
>>> [9, 0, 40]
Observe que los datos cambian entre métricas debido a que en una de ellas se considera un estado “vacío” para las cuentas. Con la función numberOfIndividuals podremos determinar cual es la cantidad de células con la que se están extrayendo las proporciones.
metricsWithoutEmptyCells.numberOfIndividuals()
>>> 9
metrics.numberOfIndividuals()
>>> 49
A continuación describiremos la segunda parte del módulo. la cual corresponde al manejo propio de los datos que se pueden extraer. Para esto debemos tener un conjunto de evoluciones del espacio de células, para lo cual nos apoyaremos del módulo epidemiologicalModelsInCA y específicamente, del modelo SIS el cuál puede consultar en el documento principal o directamente sobre el Código.
from CAsimulation import epidemiologicalModelsInCA as em
# Parámetros del modelo
alpha = 0.2
beta = 0.5
n_iterations = 10
neighborhooSystem = em.GenerateNeighborhoodSystem(csc3, "Moore")
impactRates = [1, 0.5]
SISmodel = em.SIS(alpha, beta, n_iterations, csc3, neighborhooSystem, impactRates)
evolutions = SISmodel.evolutions
evolutions
>>> [<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d6f7c41c0>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360a610>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360aa60>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360ae20>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360aac0>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360ac70>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360aaf0>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360a1f0>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d13534a30>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d13534af0>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360a100>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360abe0>]
Una vez obtenidas las evoluciones del espacio de células, la función OrderData obtener las métricas por iteración de tres maneras distintas: la primera organiza los datos en forma de tuplas o puntos, estos serán usados para graficar dichas métricas; la segunda corresponde a las propias métricas del modelo, con estos datos podremos analizar por ejemplo. el comportamiento del modelo para distintas escalas; y finalmente, la lista con las evoluciones del sistema, estos datos nos permitirán visualizar al espacio en cada iteración.
dm.OrderData(evolutions, [0, 1])
>>> [[array([[ 0., 1.],
[ 1., 1.],
[ 2., 1.],
[ 3., 1.],
[ 4., 1.],
...]),
array([[ 0., 0.],
[ 1., 0.],
[ 2., 0.],
[ 3., 0.],
[ 4., 0.],
...])],
[[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]],
[<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d6f7c41c0>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360a610>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360aa60>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360ae20>,
<EpidemiologicalModels.CellSpaceConfiguration.CellSpaceConfiguration at 0x15d1360aac0>,
...]]
Por último, presentamos a la función variationsBetweenScales con la cual podremos calcular las variaciones para distintas escalas del espacio de células, entendiendo a la escala de un espacio como la cantidad de células que lo conforma.
cellSpaceEscale1 = em.CellSpace(3,3).initialLocationOfInfected(0.5)
cellSpaceEscale2 = em.CellSpace(9,9).initialLocationOfInfected(0.5)
neighborhooSystem1 = em.GenerateNeighborhoodSystem(cellSpaceEscale1, "Moore")
neighborhooSystem2 = em.GenerateNeighborhoodSystem(cellSpaceEscale2, "Moore")
n_iterations = 10
impactRates = [1, 0.5]
evolutionsOfescale1 = em.SIS(alpha, beta, n_iterations, cellSpaceEscale1, neighborhooSystem1,
impactRates).evolutions
evolutionsOfescale2 = em.SIS(alpha, beta, n_iterations, cellSpaceEscale2, neighborhooSystem2,
impactRates).evolutions
escale1 = dm.OrderData(evolutionsOfescale1, [0,1])[1]
escale2 = dm.OrderData(evolutionsOfescale2, [0,1])[1]
dm.variationsBetweenScales(escale1[1], escale2[1])
>>> array([[ 0. , 0.14814815],
[ 1. , 0.07407407],
[ 2. , 0. ],
[ 3. , 0. ],
[ 4. , 0. ],
[ 5. , 0. ],
...])
Models
En el módulo Models podrá encontrar las reglas definidas en el documento principal. Para importarlo puede usar el siguiente comando:
from CAsimulation import Models as mo
Con el módulo SImodel podremos aplicar la regla de evolución del estado S al estado I, esto usando la función Apply del módulo, luego de haber definido los parámetros del modelo como se muestra a continuación:
cellSpace = em.CellSpace(5,5).initialLocationOfInfected(0.1)
cellSpace.system
>>> array([[0., 0., 0., 0., 1.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 1., 1., 0., 0.],
[0., 0., 0., 0., 0.]])
alpha = 0.2
beta = 0.5
neighborhoodSystems = em.GenerateNeighborhoodSystem(cellSpace, "Moore")
impactRates = [1, 0.5]
SImodel = mo.SImodel(alpha, beta, cellSpace, neighborhoodSystems, impactRates)
SImodelSpace = SImodel.Apply()
SImodelSpace.system
>>> array([[0., 0., 0., 0., 1.],
[0., 0., 1., 0., 0.],
[1., 0., 1., 0., 1.],
[1., 1., 1., 0., 0.],
[0., 0., 1., 0., 0.]])
Para aplicar los modelos SIS y SIR usaremos los mismos parámetros de la regla SI y con esto podremos generar las evoluciones por modelo para un mismo estado inicial del conjunto de células.
# Modelo SIS
SISmodel = mo.SISmodel(alpha, beta, cellSpace, neighborhoodSystems, impactRates)
SISmodel.basicRule(cellSpace).system
>>> array([[0., 0., 1., 1., 1.],
[0., 0., 0., 0., 1.],
[1., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 1., 1., 1., 0.]])
# Modelo SIR
SIRmodel = mo.SIRmodel(alpha, beta, cellSpace, neighborhoodSystems, impactRates)
SIRmodel.basicRule(cellSpace).system
>>> array([[0., 0., 1., 1., 1.],
[0., 0., 0., 1., 0.],
[0., 1., 0., 0., 0.],
[1., 1., 2., 0., 0.],
[0., 0., 1., 0., 0.]])
Para los modelos con natalidad y mortalidad; y los modelos con muerte por enfermedad, debemos incluir en nuestros parámetros a la matriz que corresponde a las edades de las células que interactuan en nuestro sistema:
ages = em.CreateAgeMatrix([[1,100,1]], cellSpace)
ages
>>> array([[19., 97., 37., 99., 9.],
[54., 19., 90., 75., 44.],
[23., 92., 54., 58., 7.],
[98., 97., 7., 92., 44.],
[37., 77., 7., 9., 99.]])
Una vez definida la matriz de edades, debemos establecer la tasa de natalidad y los rangos por muerte natural para el caso de los modelos con natalidad y mortalidad de la siguiente manera:
model = "sir" # Se aplicará el modelo SIR con natalidad y mortalidad (si desea aplicar el modelo SIS,
# remplace "sir" por "sis")
birthRate = 0.2
probabilityByAgeRanges = [[1,50,0.05], [51,100,0.08]] # Los que tienen entre 1-50 años tienen una
# probabilidad de morir del 5% y los que tienen
# entre 51 y 100, una probabilidad del 8%
timeUnit = 365 # Ciclos de 365 días
BMSIRmodel = mo.birthAndMortavility(model, alpha, beta, birthRate, [[1,100,0.05]], timeUnit, cellSpace,
neighborhoodSystems, impactRates, ages)
evolution = BMSIRmodel.basicRule(cellSpace, ages, 12)
# Evolución de los estados del sistema
evolution[0].system
>>> array([[0., 1., 0., 0., 2.],
[1., 0., 1., 0., 0.],
[1., 1., 0., 0., 0.],
[0., 1., 1., 0., 0.],
[1., 0., 3., 0., 0.]])
# Evolución de la matriz de edades
evolution[1]
>>> array([[19., 97., 37., 99., 9.],
[54., 19., 90., 75., 44.],
[23., 92., 54., 58., 7.],
[98., 97., 7., 92., 44.],
[37., 77., 0., 9., 99.]])
Si lo que desea es aplicar el modelo con muerte por enfermedad, será necesario incluir en sus parámetros las probabilidades de muerte por enfermedad por rango de edad, esto de manera análoga a como se implementaron las probabilidades de muerte para el modelo con natalidad y mortalidad.
probabilityOfDeathFromDiseaseByAgeRange = [[1,20,0.02], [21,62,0.04], [63,100, 0.08]]
DDSIRmodel = mo.deathByDisease(model, alpha, beta, birthRate, probabilityByAgeRanges,
probabilityOfDeathFromDiseaseByAgeRange, timeUnit, cellSpace,
neighborhoodSystems, impactRates, ages)
evolutionDD = DDSIRmodel.basicRule(cellSpace, ages, 12)
# Evolución de los estados del sistema
evolutionDD[0].system
>>> array([[0., 0., 1., 0., 1.],
[0., 0., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 1., 2., 0., 0.],
[3., 0., 0., 0., 0.]])
# Evolución de la matriz de edades
evolutionDD[1]
>>> array([[19., 97., 37., 99., 9.],
[54., 19., 90., 75., 44.],
[23., 92., 54., 58., 7.],
[98., 97., 7., 92., 44.],
[ 0., 77., 7., 9., 99.]])
El módulo Models también nos ofrece la posibilidad de visualizar el compartamiento de la enfermedad para una cantidad de iteraciones establecida:
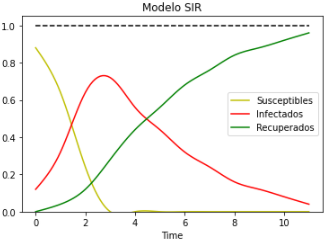
SIRmodel = mo.applyEpidemiologicalModel("sir", 0.2, 0.5, cellSpace, neighborhoodSystems, [1,0.5])
SIRmodel.basicModel(10) # 10 iteraciones
SIRmodel.plotCurvesModel("Modelo SIR", True)
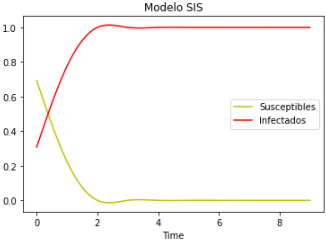
Finalmente, si lo que desea es visualizar el comportamiento promedio de la enfermedad, puede usar la clase applyEpidemiologicalModel_nIterations la cual recibe como parámetros al modelo que desea aplicar, los parámetros básicos de la enfermedad, la cantidad de simulaciones contra las que va a calcular el promedio por iteración y por último, la cantidad de iteraciones. Posteriormente puede usar la función plotCurvesModel para visualizar la evolución promedio de la enfermedad.
SISmodel = mo.applyEpidemiologicalModel_nIterations("sis", 0.2, 0.5, cellSpace, neighborhoodSystems, [1,0.5], 10, 0.2)
SISmodel.basicModel(10)
SISmodel.plotCurvesModel("Modelo SIS", False)
NeighborhoodManager
En este módulo podrá encontrar todo lo relacionado al manejo de los sistemas de vecindades, desde eun mecanismo para identificar las posiciones de las células con un rango de impacto dado hasta funciones que le permiten definir una configuración básica de estos conjuntos. Para implementarla en su entorno use la siguiente línea de código:
from CAsimulation import NeighborhoodManager as nm
Inicialmente definimos el espacio de células al cual le definiremos el sistema de vecindades como sigue:
cellSpace = em.CellSpace(5,5).initialLocationOfInfected(0.5)
cellSpace.system
>>> array([[1., 0., 0., 0., 0.],
[0., 0., 1., 1., 0.],
[1., 1., 1., 1., 1.],
[1., 0., 0., 0., 1.],
[0., 0., 0., 1., 1.]])
Para definir un sistema de vecindades para una de las células será necesario implementar la librería numpy, esto nos permitirá definir practicamente cualquier configuración para este sistema.
import numpy as np
impactMatrix = np.array([[1,2,0,1,1],[0,0,0,1,2],[4,3,1,1,2],[0,1,0,1,0],[1,2,3,4,5]])
impactMatrix
>>> array([[1, 2, 0, 1, 1],
[0, 0, 0, 1, 2],
[4, 3, 1, 1, 2],
[0, 1, 0, 1, 0],
[1, 2, 3, 4, 5]])
Con la función ImpactNeighborClassifier de la clase NeigborhoodManager podremos conocer los estados y las posiciones de las células por grado de impacto en forma de diccionario.
NeigborhoodManager·=·nm.NeigborhoodManager(cellSpace,·impactMatrix)
NeigborhoodManager.ImpactNeighborClassifier()
>>> {0: [[0.0, [0, 2]], [0.0, [1, 0]], [0.0, [1, 1]],
[1.0, [1, 2]], [1.0, [3, 0]], [0.0, [3, 2]],
[1.0, [3, 4]]],
1: [[1.0, [0, 0]], [0.0, [0, 3]], [0.0, [0, 4]],
[1.0, [1, 3]], [1.0, [2, 2]], [1.0, [2, 3]],
[0.0, [3, 1]], [0.0, [3, 3]], [0.0, [4, 0]]],
2: [[0.0, [0, 1]], [0.0, [1, 4]], [1.0, [2, 4]],
[0.0, [4, 1]]],
3: [[1.0, [2, 1]], [0.0, [4, 2]]],
4: [[1.0, [2, 0]], [1.0, [4, 3]]],
5: [[1.0, [4, 4]]]}
Ahora, si lo que desea es definir un sistema de vecindades “básico”, puede usar alguna de las tres funciones: Moore, Von_Neumann o randomNeighborhoods como se muestra a continuación:
cellSpace = em.CellSpace(3,3)
nm.Moore(cellSpace)
>>> [[[0, 0], array([[0., 0., 1.], [0., 0., 1.], [1., 1., 1.]])],
[[0, 1], array([[0., 0., 0.], [0., 0., 0.], [1., 1., 1.]])],
[[0, 2], array([[1., 0., 0.], [1., 0., 0.], [1., 1., 1.]])],
[[1, 0], array([[0., 0., 1.], [0., 0., 1.], [0., 0., 1.]])],
[[1, 1], array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]])],
[[1, 2], array([[1., 0., 0.], [1., 0., 0.], [1., 0., 0.]])],
[[2, 0], array([[1., 1., 1.], [0., 0., 1.], [0., 0., 1.]])],
[[2, 1], array([[1., 1., 1.], [0., 0., 0.], [0., 0., 0.]])],
[[2, 2], array([[1., 1., 1.], [1., 0., 0.], [1., 0., 0.]])]]
nm.Von_Neumann(cellSpace)
>>> [[[0, 0], array([[0., 0., 1.], [0., 1., 1.], [1., 1., 1.]])],
[[0, 1], array([[0., 0., 0.], [1., 0., 1.], [1., 1., 1.]])],
[[0, 2], array([[1., 0., 0.], [1., 1., 0.], [1., 1., 1.]])],
[[1, 0], array([[0., 1., 1.], [0., 0., 1.], [0., 1., 1.]])],
[[1, 1], array([[1., 0., 1.], [0., 0., 0.], [1., 0., 1.]])],
[[1, 2], array([[1., 1., 0.], [1., 0., 0.], [1., 1., 0.]])],
[[2, 0], array([[1., 1., 1.], [0., 1., 1.], [0., 0., 1.]])],
[[2, 1], array([[1., 1., 1.], [1., 0., 1.], [0., 0., 0.]])],
[[2, 2], array([[1., 1., 1.], [1., 1., 0.], [1., 0., 0.]])]]
nm.randomNeighborhoods(cellSpace)
>>> [[[0, 0], array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.]])],
[[0, 1], array([[1., 0., 1.], [1., 1., 1.], [1., 1., 1.]])],
[[0, 2], array([[1., 1., 0.], [1., 1., 1.], [1., 1., 1.]])],
[[1, 0], array([[1., 1., 1.], [0., 1., 1.], [1., 1., 1.]])],
[[1, 1], array([[1., 1., 1.], [1., 0., 1.], [1., 1., 1.]])],
[[1, 2], array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.]])],
[[2, 0], array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.]])],
[[2, 1], array([[1., 1., 1.], [1., 1., 1.], [1., 0., 1.]])],
[[2, 2], array([[1., 1., 1.], [1., 1., 1.], [1., 1., 0.]])]]
PlotsManager
Como su nombre lo indica, PlotsManager se encarga del manejo de las gráficas dado un conjunto de datos. Para imprtarla simplemente debemos ejecutar el siguiente script:
from CAsimulation import PlotsManager as pm
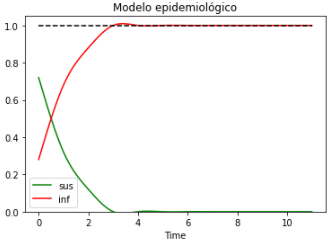
Inicialmente debemos establecer el conjunto de datos en forma de listas de coordenadas. Para nuestro ejemplo usaremos los datos generados por el modelo SIS, y para visualizar dicha información, usaremos la función plotSolutions.
cellSpace = em.CellSpace(5,5).initialLocationOfInfected(0.3)
neighborhoodSystems = em.GenerateNeighborhoodSystem(cellSpace, "Moore")
SImodel = mo.applyEpidemiologicalModel("sis",0.2, 0.5, cellSpace, neighborhoodSystems, [1,0])
SImodel.basicModel(10)
pm.plotSolutions(SImodel.data, ["sus", "inf"], ["green", "red"], "Modelo epidemiológico", True)
SystemVisualization
Con este módulo podremos visualizar los diferentes comportamientos dentro de nuestro sistema por iteración. Para implementarlo podemos ejecutar la siguiente línea:
from EpidemiologicalModels import SystemVisualization as sv
Al igual que con el módulo plotSolutions, debemos definir inicialmente al conjunto de datos. Nosotros usaremos como caso particular a los datos que se puden obtener al aplicar el modelo SIS como se muestra a continuación:
# Importamos los módulos necesarios para generar los datos
from EpidemiologicalModels import epidemiologicalModelsInCA as em
from EpidemiologicalModels import Models as mo
cellSpace = em.CellSpace(5,5).initialLocationOfInfected(0.3)
neighborhoodSystems = em.GenerateNeighborhoodSystem(cellSpace, "Moore")
SImodel = mo.applyEpidemiologicalModel("sis",0.2, 0.5, cellSpace, neighborhoodSystems, [1,0])
SImodel.basicModel(10)
SystemVisualization = sv.SystemVisualization(SImodel.evolutions)
SystemVisualization.evolutionsPlot(2) # Visualización del espacio en la segunda iteración
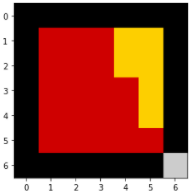
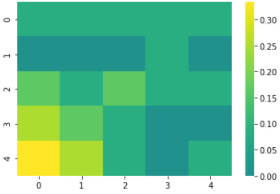
SystemVisualization también nos ofrece la posibilidad de visualizar el mapa de calor que muestra el cambio por estado en el sistema. Como caso particular usaremos el estado S (identificado con 0):
SystemVisualization.heatmap(0)
epidemiologicalModelsInCA
Hemos usado al módulo epidemiologicalModelsInCA en diferentes secciones de la documentación por lo que seguramente podrá apreciar que algunos de los métodos que expondremos durante esta sección. El objetivo de este módulo es facilitar la implementación de la librería, es por esto que muchos de las funciones que mostraremos son una versión “simplificada” heredada de otros módulos. Para implementar esta librería puede ejecutar la siguiente línea:
from CAsimulation import epidemiologicalModelsInCA as em
Con la función CellSpace podremos definir el espacio de células de manera similar a como se implementó la función CellSpaceConfiguration expuesta en el módulo con el mismo nombre.
space = em.CellSpace(10,10)
space.system
>>> array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
space = em.CellSpace(3,1,5,5)
space.system
>>> array([[ 0., -1., -1., -1., -1.],
[ 0., -1., -1., -1., -1.],
[ 0., -1., -1., -1., -1.],
[-1., -1., -1., -1., -1.],
[-1., -1., -1., -1., -1.]])
space = em.CellSpace(3,1,5,5,1,2)
space.system
>>> array([[-1., -1., -1., -1., -1.],
[-1., -1., 0., -1., -1.],
[-1., -1., 0., -1., -1.],
[-1., -1., 0., -1., -1.],
[-1., -1., -1., -1., -1.]])
También puede crear la matriz de edades dados un conjunto de rangos de edad y un espacio de células con la función createAgeMatrix.
ranges = [[0,10,0.2],[11,100,0.8]] # 20% tienen entre 0 y 10 años, y 80% tienen entre 11 y 100.
space = CellSpace(5,5)
em.createAgeMatrix(ranges, space)
>>> array([[ 1., 81., 33., 5., 18.],
[90., 19., 18., 36., 50.],
[ 5., 67., 4., 18., 74.],
[45., 36., 4., 36., 4.],
[ 5., 67., 74., 1., 1.]])
Si lo que desea es generar un sistema de vecindades usual, puede utilizar la función GenerateNeighborhoodSystem como sigue:
em.GenerateNeighborhoodSystem(CellSpace(3,3),"Moore")
>>> [[[0, 0],array([[0., 0., 1.], [0., 0., 1.], [1., 1., 1.]])],
[[0, 1],array([[0., 0., 0.], [0., 0., 0.], [1., 1., 1.]])],
[[0, 2],array([[1., 0., 0.], [1., 0., 0.], [1., 1., 1.]])],
...]
Si desea aplicar alguno de los modelos de la librería debe definir inicialmente los parámetros del mismo, a continuación mostramos un apartado con la implementación de cada uno de los modelos:
# Parámetros generales
cellSpace = CellSpace(9,9).initialLocationOfInfected(0.1)
neighborhoodSystem = GenerateNeighborhoodSystem(cellSpace,"moore")
alpha = 0.2
beta = 0.5
n_iterations = 10
impactRates = [1,0]
# Modelos SIS y SIR
sis = SIS(alpha, beta, n_iterations, cellSpace, neighborhoodSystem, impactRates)
sir = SIR(alpha, beta, n_iterations, cellSpace, neighborhoodSystem, impactRates)
# Parámetros para modelos con edades
birthRate = 0.2
rangesOfDeadProbability = [[0,20,0.0005], [21,58,0.0008], [59,100,0.001]]
ageMatrix = CreateAgeMatrix([[0,100,1]], cellSpace)
timeUnit = 365 # 365 días
# Modelos con natalidad y mortalidad
sis_bm = SIS_BM(alpha,beta,birthRate,rangesOfDeadProbability,timeUnit,n_iterations,cellSpace,
neighborhoodSystem,impactRates,ageMatrix)
sir_bm = SIR_BM(alpha,beta,birthRate,rangesOfDeadProbability,timeUnit,n_iterations,cellSpace,
neighborhoodSystem,impactRates,ageMatrix)
# Parámetros para modelos con muerte por enfermedad
deadByDiseaseProbabilities = [[0,15,0.005], [16,60,0.009], [61,70,0.01], [71,100,0.06]]
# Modelos con muerte por enfermedad
sis_dd = SIS_DD(alpha,beta,birthRate,rangesOfDeadProbability,deadByDiseaseProbabilities,timeUnit,
n_iterations,cellSpace,neighborhoodSystem,impactRates,ageMatrix)
sir_dd = SIR_DD(alpha,beta,birthRate,rangesOfDeadProbability,deadByDiseaseProbabilities,timeUnit,
n_iterations,cellSpace,neighborhoodSystem,impactRates,ageMatrix)
También puede aplicar los modelos y generar sus datos promedios para una cantidad de simulaciones definida. En el siguiente fragmento de código podremos apreciar como se pueden implementar este tipo de funciones:
# Parámetros generales
alpha = 0.2
beta = 0.5
initialInfectedPopulation = 0.1
n_iterations = 10
n_simulations = 3
cellSpace = CellSpace(9, 9).initialLocationOfInfected(0.1)
neighborhoodSystem = GenerateNeighborhoodSystem(cellSpace, "moore")
impactRates = [1,0]
# Modelos SIS y SIR
medium_sis = medium_SIS(alpha,beta,initialInfectedPopulation,n_iterations,n_simulations,cellSpace,
neighborhoodSystem,impactRates)
medium_sir = medium_SIR(alpha,beta,initialInfectedPopulation,n_iterations,n_simulations,cellSpace,
neighborhoodSystem,impactRates)
# Parámetros para modelos que consideran las edades del sistema
birthRate = 0.2
rangesOfDeadProbability = [[0,20,0.0005], [21,58,0.0008], [59,100,0.001]]
timeUnit = 365 # 365 días = 1 año
ageMatrix = CreateAgeMatrix([[0,100,1]], cellSpace)
# Modelos con natalidad y mortalidad
medium_sis_bm = medium_SIS_BM(alpha,beta,birthRate,rangesOfDeadProbability,timeUnit,
initialInfectedPopulation,n_iterations,n_simulations,cellSpace,
neighborhoodSystem,impactRates,ageMatrix)
medium_sir_bm = medium_SIR_BM(alpha,beta,birthRate,rangesOfDeadProbability,timeUnit,
initialInfectedPopulation,n_iterations,n_simulations,cellSpace,
neighborhoodSystem,impactRates,ageMatrix)
# Parámetros para modelos con muerte por enfermedad
deadByDiseaseProbabilities = [[0,15,0.005], [16,60,0.009], [61,70,0.01], [71,100,0.06]]
# Modelos con muerte por enfermedad
medium_sis_dd = medium_SIS_DD(alpha,beta,birthRate,rangesOfDeadProbability,deadByDiseaseProbabilities,
timeUnit,initialInfectedPopulation,n_iterations,n_simulations,cellSpace,
neighborhoodSystem,impactRates,ageMatrix)
medium_sir_dd = medium_SIR_DD(alpha,beta,birthRate,rangesOfDeadProbability,deadByDiseaseProbabilities,
timeUnit,initialInfectedPopulation,n_iterations,n_simulations,cellSpace,
neighborhoodSystem,impactRates,ageMatrix)